Spotlight on spectral flow: Matthias Lesch
SMRI’s first visitor Matthias Lesch investigates spectral flow in the language of Clifford algebras

SMRI’s first international visitor Matthias Lesch and his Australian collaborators have recently published a paper on spectral flow in the Journal of Topology and Analysis, published by World Scientific.
Based at the Mathematical Institute of the University of Bonn, Professor Dr. Lesch’s research focuses on geometric differential operators and their spectral theory. Lesch spent three months in New South Wales in May–July of 2019.
His visit to SMRI was hosted by the former Head of the University of Sydney’s School of Mathematics and Statistics, Jacqui Ramagge. Lesch followed his stay in Sydney with a visit to the University of Wollongong hosted by his co-authors, Adam Rennie and Alan Carey. The fourth co-author of the paper, KO-valued spectral flow for skew-adjoint Fredholm operators, is Chris Bourne from Tohoku University, previously at The Australian National University.
‘I had three wonderful months Down Under,’ recalls Lesch. ‘I only had to write on the paper, watch the cockatoos over my morning coffee, hike in the wonderful outdoors around Sydney and Wollongong, and I met a lot of wonderful people.’
Making connections between spectral flow and real K-theory
Spectral flow is a classical notion of functional analysis and differential geometry that has been given different interpretations. It is of particular interest for mathematicians working on partial differential equations, as well as those working in mathematical physics. Lesch’s interest in spectral flow is grounded in the index theory of Michael Atiyah, Vijay Kumar Patodi and Isadore Singer in the 1960s and 1970s. These mathematicians established index theory on manifolds with boundary, an edge condition that introduces restrictions. Atiyah was awarded a Fields Medal for his work in 1966.
Index theory mainly looks to provide index formulas for Fredholm operators, a linear operator mapping certain function spaces into another. Lesch describes spectral flow ‘as an interesting mathematical object: a priori, it is an integer like the Fredholm index.’
The celebrated Atiyah-Singer Index Theorem postulates a deep connection between certain spectral invariants and topological K-theory. The latter has its origin in topology and was founded to study vector bundles on topological spaces. ‘Generally speaking, K-theory is a cohomology theory which classifies vector bundles,’ explains Lesch.
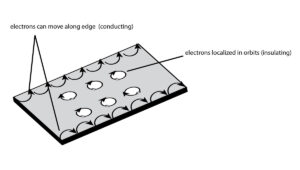
Spectral theory also lies at the heart of quantum theory – hence its importance for mathematical physicists. K-theory is believed to play an important role in the mathematical background of topological insulators. These materials have an insulating interior, but with a surface that contains conducting states (meaning electrons can only move along the material’s surface). The materials have been the subject of many recent papers in condensed-matter physics.
One of the overarching aims of this paper was to unify the various notions of spectral flow and show that they all arise as the spectral flow of a system with a certain number of Clifford symmetries. Clifford algebras are connected with the theory of quadratic forms and orthogonal transformations, with important applications in quantum theory.
Previous work by Bourne, Carey and Rennie refined the use of Clifford algebras in the description of topological phases of matter. The new ingredient in this paper is a description of the geometry of the momentum space, or Brillouin zone, using Kasparov’s generalisation of K-theory. With this formulation, they could give a comprehensive description of the relationship between bulk conductivity and edge current states of condensed matter systems. ‘These results were a primary motivation for understanding spectral flow in the same level of generality,’ says Rennie.
For Lesch, the motivation for this work was to clarify the deep connections between several unrelated objects: several versions of a priori constructed spectral flows and KO-valued indices. K refers to K-theory, while O refers to the structure group (the real general linear group). In ordinary K-theory the structure group is not mentioned: it is the complex general linear group.
The authors developed the notion of a general KO-valued spectral flow that incorporates systems with symmetries. One of the motivating factors is the recent applications of the study of spectral flow on topological phases of matter, which show that Fredholm indices take their “true” value in K-theory. Therefore, ‘it is absolutely clear that there must be an analogue of the spectral flow in real K-theory,’ says Lesch.
Two strange spectral flows
The paper focuses on two “strange”-valued spectral flows know to physicists, Z and Z/2Z. In theoretical physics, the index of skew-adjoint Fredholm operators are used to characterise the topological phases of fermionic systems. ‘The structures involved go back to Atiyah. They are so beautiful that when I saw the first papers on Z/2Z spectral flow, it was clear to me that this paper had to be written,’ says Lesch.
This work operates on the principle that spectral flow is equal to the Fredholm index. ‘All one needs to do is to formulate things consequently in the language of K-theory and then it turns out that the Z/2Z valued spectral flows naturally fit into the theory,’ explains Lesch.
The authors comprehensively characterise a spectral flow for loops in the space of skew-adjoint Fredholm operators on a real Hilbert vector space. This notion of a “Clifford module flow” was first described by Witten. ‘I think that the main strength of the paper is that we give a comprehensive treatment of all aspects of a theory, which has been a bit scattered in the literature,’ says Lesch. ‘What is new is that the spectral flow is developed consequently in the language of Clifford algebras.’
The authors found that KO-valued spectral flow relates to a KO-valued index by proving a Robbin-Salamon type result, which refers to the interpretation of the index theorems related to Kasparov theory. The Robbin-Salamon theorem was obtained in a similar manner to the relation between bulk and edge states for topological insulators using the Kasparov product. `Describing the physical (or geometric) parameters in a way that is compatible with Clifford variables allows the Kasparov product to be computed relatively easily,’ says Bourne.
Lesch believes that the significance of the paper lies in its extensive treatment of spectral flow theory and its direct application to topological condensed matter systems. ‘I hope that in the long run this paper will be a main reference for the subject,’ says Lesch.
Read the first research profile in this series “Spotlight on network dynamics: Bob Rink”.
- Interview with Jessica Fintzen - 2024 March 20
- “Geometry: the archetype of beauty” public lecture and photo gallery - 2024 March 15
- Pi Day 2024: public lecture & Sydney high school workshops - 2024 February 6

