SMRI visitor Bob Rink investigates multiple timescales in recent publications

Past SMRI visitor Bob Rink and his collaborators have recently published three papers related to Rink’s research visit to SMRI in the journal Nonlinearity, published by the London Mathematical Society.
Professor of mathematics at the Vrije Universiteit Amsterdam, Rink carries out research in nonlinear analysis and dynamical systems, with a focus on network dynamical systems, bifurcation theory and Aubry-Mather theory. Rink visited SMRI over January–July 2020 as part of the 2019 International Visitor Program, and his family was able to join him for the visit in Sydney.
Due to the pandemic, Rink spent part of his visit working independently on a paper on Quiver representations in dynamical systems (SIAM Journal on Applied Dynamical Systems). Nevertheless, he also managed to strike up a collaboration with University of Sydney mathematicians Martin Wechselberger and Ian Lizarraga. The three co-authors published the Nonlinearity paper Multiple timescales and the parametrisation method in geometric singular perturbation theory in June 2021.
Computing multiple timescales
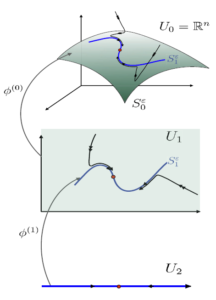
The paper focuses on systems that evolve on multiple timescales. This temporal feature is often seen in biological and physical systems because many processes take place on different timescales. In some chemical reactions for example, some of the chemicals are used up quicker than others, after which the reaction continues at a slower rate and involves different reaction mechanisms. Mathematically, such systems can be described by so-called singular perturbation problems.
University of Sydney Professor Martin Wechselberger’s research group, which includes postdoctoral researcher Dr Ian Lizarraga, has world expertise on multiple timescale problems; in particular coordinate-independent geometric singular perturbation theory (GSPT). The paper combines their expertise with Bob’s work on the parametrisation method, and it has laid the foundations for this general algorithmic approach to study genuine multiple timescale problems (those with three or more distinct timescales).
The authors present a novel method for computing slow manifolds, the regimes in which the system evolves considerably slower than elsewhere. Broadly speaking, parametrisation is a method of computing and approximating low-dimensional structures in complex systems. This study is the first time a parametrisation method has been used for multiple timescale systems.
Compared to older, more commonly used methods such as computational singular perturbation method (CSTP), the parametrisation method can also compute “infra slow” dynamics and beyond. This term refers to dynamics that evolves on an even slower timescale than the slow dynamics. The authors present a top-down, multi-scale algorithm to detect dynamics evolving on multiple timescales. Surprisingly, the number of those timescales might be larger than the number of multi-scale processes given by the model. ‘We call these “hidden timescales”, as they cannot be easily predicted but require quite lengthy computations,’ says Rink.
‘The strength of the parametrisation method is that it provides a clear algorithmic approach to multi-scale GSPT,’ says Wechselberger. It currently covers the generic, normally hyperbolic, case where cascading dynamics from the fastest via the intermediate to the slowest timescale is expected. The mathematicians hope to apply their parametrisation method to other reaction network problems, and potentially to certain problems in neuroscience too.
Unique approaches to networks
In recent years, Rink’s research focus has been on network dynamical systems and the mathematical tools that analyse them. Research in network dynamics has exploded in recent years, particularly the study of synchronisation and its application in neuroscience. Other hot topics relate to generalisations such as “hypernetworks” that go beyond pairwise interaction. Rink uses the example of opinion networks, such as in a circle of friends or social media group, in which peer pressure is relevant for the formation or absence of consensus.
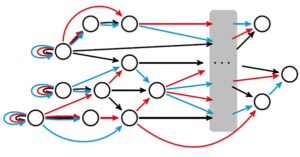
‘To my surprise not much of the work on network dynamics is very mathematical,’ remarks Rink. ‘Nor is there a lot of math developed specifically for network dynamics.’ But researchers who do work in this area now try to make links with other areas of mathematics. Examples include category theory, or groupoids, such as Ian Stewart and Marty Golubitsky.
Rink and his colleagues are particularly interested in dynamical systems with the underlying structure of a network, which are called coupled cell systems. ‘Almost every deterministic system found in nature or engineering is of this form (the solar system, interacting particles, competing species, reacting chemicals, you name it),’ says Rink.
The term itself was coined by Stewart and Golubitsky in the early 2000s, who started systematically studying synchronisation patterns in these coupled cell systems. They were led to this idea because of their previous work on systems with symmetry.
Systems with symmetry often feature synchronisation, and Rink and his Vrije Universiteit colleague Jan Sanders were the first to realise that certain network structures can be described as a generalisation of symmetry. This is not the classical type of group of symmetry, as the symmetry structure is often that of a semigroup, or a quiver. ‘This symmetry can then be exploited to predict synchronisation, and, as in the case of the Nonlinearity paper, synchrony-breaking,’ explains Rink.
This was a “Eureka moment” for Rink and his colleagues. ‘People had been observing synchronisation in networks for a long time, as well as anomalous synchrony-breaking, and everyone had seen the similarity with what happens symmetric systems, but we were the first who were able to pinpoint the actual symmetries that are responsible for it,’ he says.
Rink now hopes to combine his work on networks with the recent results on slow-fast systems. He believes that using generalised symmetry methods may lead to new insights in networks with a slow-fast structure. Specifically, this may yield new ways to perform high-order phase reduction (a popular technique in mathematical neuroscience) for networks of coupled oscillators.
Coupled oscillators are any system of connected, periodically evolving systems, as may arise in molecules, acoustics, structural vibrations and coupled electrical circuits. ‘It’s a really cool field, and by now I’m quite sure our methods will actually work to predict slow-fast synchronisation patterns,’ says Rink.
Read the next research profile in this series: Spotlight on spectral flow: Matthias Lesch.

